


|

|
Jetzt haben wir das Grundlegende zur Funktionenprogrammierung gelernt. Es gibt in QBASIC noch ein paar andere Konzepte, wie z.B. SHARED-Variablen, die aber eher unelegante Krückstöcke für Konzepte der strukturierten Programmierung sind, die in moderneren BASIC-Implementationen (und erst recht in anderen Sprachen wie PASCAL, Java oder Python) besser umgesetzt wurden. Daher ist es sinnvoller, sich damit erst im nächsten Teil zu beschäftigen.
Damit Sie aber ein Gefühl dafür entwickeln, wie mächtig die Werkzeuge sind, die Sie in den letzten Kapiteln gelernt haben, sollen Sie abschliessend für diesen Teil ein Übungsprogramm erstellen, bei dem Sie vermutlich nicht annehmen, dass Sie das schaffen könnten: Eine 3D-Animation. Ein Körper soll im dreidimensionalen Raum um eine beliebige Achse gedreht werden können.
Die einzige grosse Kunst bei dieser Übung ist es, die grosse Aufgabe in kleine Aufgaben zu zerlegen, die wir jede in einer eigenständigen Funktion lösen können. Dann müssen wir die Funktionen nur noch richtig "zusammenstöpseln" - und das war's.
Es sei vorweggenommen: Natürlich gibt es heute für diese Aufgabe komfortable Ressourcen (DirectX, OpenGL). Aber erstens sind diese für QBASIC nur schwer zugänglich und zweitens macht es ja auch Spass, zu sehen, wie diese Ressourcen intern dem Prinzip nach funktionieren.
Fangen wir mal ganz einfach an: Ein Punkt im dreidimensionalen Raum - wie zeichne ich den, wenn meine Zeichnung doch eigentlich nur zweidimensional sein kann? Wir müssen hier zwischen der dreidimensionalen Welt "hinter" dem Bildschirm unterscheiden und dem 2-dimensionalen Abbild der Welt auf dem Bildschirm. Ein ganz zentraler Trick wird sein, ersteinmal alle Operationen im 3-dimensionalen Weltkoordinatensystem (Weltsystem) auszuführen und erst am Schluss uns darum zu kümmern, wie wir das nun ins 2-dimensionale Bildkoordinatensystem (Screen) überführen.
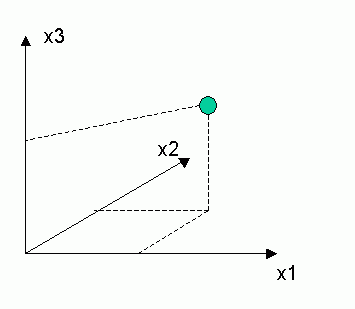
Jeder Punkt hat im Weltsystem Koordinaten (x1,x2,x3). Wir betrachten dieses Weltsystem aus einer bestimmten (fixen, isometrischen) Perspektive, in der die Achse x2 in die Screenebene hineinzeigt und damit in die Screenebene "übersetzt" werden muss. Die Koordinaten x1 und x3 entsprechen also zunächst denen des Screens. Aber dann müssen wir von dort im Winkel der x2-Achse zur x1-Achse weiterlaufen. Nennen wir diesen α. Und zwar um die Strecke x2*cos(α) in Richtung x1 und um die Strecke x2*sin((α) in Richtung x3. Damit ist die ganze Übersetzung fertig:
Die Zahl in Klammern gibt jeweils an, zu welchem System die Koordinate gehört, (2) ist das Bildschirmsystem, (3) ist das dreidimensionale Weltsystem.
α ist eine Systemkonstante, die unseren Blickwinkel angibt. (Dieser soll nicht veränderlich sein.) Ein Wert für Alpha, der gut aussieht, ist 66 Grad.
Die erste Funktion, die wir also programmieren können, ist eine, die zu einem 3D-Punkt die Koordinaten auf dem 2D-Schirm liefert. Nennen wir sie coords3d(x1,x2,x3). Da zwei Koordinaten zurückgegeben werden müssen (x und y für den Screen), machen wir zwei Funktionen draus: coords3dx%(x1,x2,x3) und coords3dy%(x1,x2,x3). (Das Prozentzeichen, weil die Funktionen INTEGER-Werte zurückgeben.) Jede Funktion entspricht einer der obigen Formeln.
...sind nun sehr, sehr einfach. Unser line3D-Befehl setzt einfach in den LINE-Befehl von QBASIC die coords3dx%- und coord3dy%-Funktion für Anfangs- und Endpunkt der Linie ein und fertig.
Ein Hinweis: Wenn Sie jetzt losschreiben (und das sollten Sie), dann benutzen Sie bitte Screen 9. Das hat seinen Grund weiter unten...
Mit Hilfe unseres line3D-Befehls können wir nun leicht ein 3-dimensionales Koordinatensystem zeichnen:

, hier gleich noch mit einer 3D-Linie darin.
Die Funktion, die dieses Koordinatensystem zeichnet, nennen wir "coordsys".
Man kann aber schon nettere Sachen machen. Z.B. eine dreidimensionale Spirale. Dazu lassen wir x1 und x2 einen Kreis beschreiben, während x3 in die Höhe wandert:
FOR i = 0 TO 1000
y1 = INT(100 * SIN(i / 20 * 22 / 7) + .5)
y2 = INT(100 * COS(i / 20 * 22 / 7) + .5)
y3 = INT((i - 500) / 5 + .5)
IF (i = 0) THEN
x1 = y1: x2 = y2: x3 = y3
END IF
CALL LINE3d(x1, x2, x3, y1, y2, y3, 15)
END
Das sieht dann so aus:

Allerdings werden wir merken, dass das Hantieren mit jeweils 3 Koordinaten für jeden 3D-Punkt mit der Zeit etwas umständlich wird. Daher führen wir einen neuen Datentyp ein:
TYPE POINT3dtyp x1 AS DOUBLE x2 AS DOUBLE x3 AS DOUBLE END TYPE
x1, x2 und x3 haben wir bewusst als Fliesskommazahl mit hoher Genauigkeit gewählt. Für die später auszuführenden Bewegungen und Rotationen werden viele Additionen und Multiplikationen erforderlich. Da kommt es leicht zu Rundungsungenauigkeiten, die sich dann anhäufen und schliesslich das Bild verzerren, wenn wir die innere Rechengenauigkeit zu niedrig wählen.
Diese nimmt nicht sechs Einzelkoordinaten, sondern zwei 3D-Punkte entgegen:
SUB LINE3dp (p1 AS POINT3dtyp, p2 AS POINT3dtyp, col1 AS INTEGER)Ist doch schick, oder?
Das Problem, eine Figur in 3D darzustellen, gehen wir so an, dass wir diese Figur aus lauter viereckigen Klötzen darstellen wollen. In diesem Beispiel beschränken wir uns auf die Darstellung eines Klotzes. Wie beschreiben wir den Klotz? Nun, ein solcher Klotz hat acht Eckpunkte. Und 3D-Punkte haben wir ja schon. Also nichts einfacher als das:
TYPE cubetyp p1 AS POINT3dtyp p2 AS POINT3dtyp p3 AS POINT3dtyp p4 AS POINT3dtyp p5 AS POINT3dtyp p6 AS POINT3dtyp p7 AS POINT3dtyp p8 AS POINT3dtyp END TYPE
...und schon ist er fertig. Wollen wir einen solchen Klotz zeichnen, müssen wir nur zwölf Linien zeichnen: Mit jeweils vier Linien zeichnen wir "Boden" und "Deckel" des Klotzes, die z.B. von p1,p2,p3,p4 und p5,p6,p7,p8 dargestellt werden. Und dann verbinden wir jeweils eine E Ecke des Bodens mit einer Ecke des Deckels, also p1 mit p5, p2 mit p6 usw. Macht zwölf Linien, die mit Hilfe von line3dp() schnell geschrieben sind.
Die Frage ist allerdings, wie wir die Eckpunktkoordinaten bestücken. Das sind doch immerhin jetzt 24 Koordinaten! Eine gute Idee ist, sich einen Stützpunkt auszusuchen. In meinem Kopf z.B. ist es immer der vordere untere linke Punkt. Dies sei p1. Und dessen Lage geben wir an. Z.B. legen wir ihn einfach in den Nullpunkt: p1.x1=0 : p1.x2=0 : p3.x3=0. Dann definieren wir eine Funktion, die nennen wir einfach "cubeinit". Also initialisiere den Klotz. Und zwar mit drei Angaben: Breite, Länge, Höhe. Anfangs soll der Klotz so liegen, dass die Breite in die x1-Richtung (nach rechts) geht, die Länge in die x2-Richtung und die Höhe natürlich in die Höhe (x3). cubeinit(breite, laenge, hoehe) nimmt uns dann die Initialisierung der restlichen sieben Punkte ab.
Und siehe da, wir können unseren ersten Klotz zeichnen!

Als nächstes wollen wir Bewegung ins Spiel bringen. Wir fangen einfach an und verschieben erst einmal den Klotz. In sechs mögliche Richtungen. Die Funktion nennen wir "movecube3d":
SUB movecube3d(cube AS cubetype, dx AS POINT3dtyp)
In dx sind die drei Schrittgrössen in x1, x2 und x3-Richtung gespeichert. In der Mathematik nennt man einen solchen "Raumschritt" auch einen "Vektor". Mit solchen Vektoren bekommen wir es bei der Rotation nochmal zu tun. Hier ist aber alles einfach: Einfach die jeweilige Koordinate von dx auf die jeweilige Koordinate aller Punkte des Klotzes draufaddieren und dann alles neu zeichnen. Fertig. Damit das richtig schön dynamisch wird, sollten wir unser movecube3d von einer Tastaturschleife aus aufrufen:
DIM cube AS cubetype DIM dp AS POINT3dtyp cube.p1.x1=0 cube.p1.x2=0 cube.p1.x3=0 CALL cubeinit(cube,20,20,100) CALL cubedraw(cube) 'Das ist die Funktion, die die zwölf Linien malt. a$ = "" ascreen = 0 WHILE (a$ <> "q") a$ = "" WHILE (a$ = ""): a$ = INKEY$: WEND IF (a$ = CHR$(0) + "M") THEN dp.x1=3:dp.x2=0:dp.x3=0:CALL movefig3d(cube,dp) IF (a$ = CHR$(0) + "K") THEN dp.x1=-3:dp.x2=0:dp.x3=0:CALL movefig3d(cube,dp) IF (a$ = CHR$(0) + "P") THEN dp.x1=0:dp.x2=3:dp.x3=0:CALL movefig3d(cube,dp) IF (a$ = CHR$(0) + "H") THEN dp.x1=0:dp.x2=-3:dp.x3=0:CALL movefig3d(cube,dp) IF (a$ = "t") THEN dp.x1=0:dp.x2=0:dp.x3=3:CALL movefig3d(cube,dp) IF (a$ = "g") THEN dp.x1=0:dp.x2=0:dp.x3=-3:CALL movefig3d(cube,dp) WEND
Damit können wir den Klotz in allen drei Dimensionen über den Bildschirm bewegen:
Bitte beachten: Innerhalb von movefig3d() muss nochmals cubedraw() aufgerufen werden und cubedraw() muss immer alles neu zeichnen. Also "CLS" und dann das Koordinatensystem (sofern man es haben möchte) und den ganzen Klotz.
Das können wir natürlich nur deswegen so machen - und auch nur deswegen ist die Aufgabe für uns jetzt in BASIC relativ einfach bewältigbar - weil unser Rechner so irre schnell ist, dass er das locker in Millisekunden hinkriegt.
Das mit den Verschieben funktioniert, solange wir nur einmal pro Sekunde eine Cursortaste drücken. Wenn wir sie aber gedrückt halten, dann bewegt sich die Figur zwar, aber sie wird nicht mehr richtig gezeichnet. Wir sehen sie kaum noch. Das liegt daran, dass die Figur die meiste Zeit gar nicht da oder im halb gezeichneten Zustand ist. In der Millisekunde, in der sie fertig ist, wird sie ja schon wieder gelöscht.
Was können wir da machen? Die entsprechende Lösung heisst "Double Buffering". Wie wir schon im ersten Teil bei der Grafikprogrammierung erfahren haben, benötigt der Computer zur Darstellung des Screens Speicher. Die Grafikkarte nimmt diesen Speicherinhalt und bildet ihn laufend (ca. 60 bis 100 Mal in der Sekunde) auf dem Monitor ab. Nun gibt es die Möglichkeit, einen kompletten zweiten solchen Speicher zu reservieren. Ob das technisch auch geht, hängt von der verwendeten Grafikkarte ab - bzw. vom Grafikkartenstandard, den QBASIC ansteuert. Dieser EGA/VGA-Standard, den QBASIC nur kennt, ist schon ein bisschen alt und daher gibt es diesen doppelten Speicher nicht bei allen Betriebsmodi, nicht z.B. bei SCREEN 12 oder SCREEN 13, sehr wohl aber bei SCREEN 9. Und den haben wir ja wohlweislich genommen.
Man nennt solche Speicher "Bildschirmseiten". Wir reservieren also zwei Bildschirmseiten. Eine wird dargestellt und eine ist versteckt im Hintergrund. Der Clou ist nun, dass wir auch auf diese versteckte Seite zeichnen können. Wir bauen also das Bild auf der versteckten Seite auf. Und erst wenn es fertig ist, schalten wir es sichtbar (und wechseln gleichzeitig mit dem Zeichnen auf die andere, nun unsichtbare Seite.) Das Zeichnen geschieht auf diese Art und Weise im Hintergrund und es wird im Vordergrund immer eine fertige Zeichnung angezeigt. Daher flackert des Bild nicht mehr.
Das Reservieren und Ansteuern der Bildschirmseiten geschieht alles mit dem SCREEN-Befehl:
| Reservieren: | SCREEN 9. Das impliziert schon zwei Bildschirmseiten. By default wird Seite 0 angezeigt und auf Seite 0 gezeichnet |
| Zeichnen: | SCREEN 9,, |
Das Zeichnen muss jetzt also so geschehen, dass in einer Variablen die dargestellte Seite gespeichert ist. Nennen wir sie ascreen. Sie hat den Wert null oder eins. Vor dem Zeichnen muss als aktive Seite 1-ascreen eingestellt werden. Dann wird gezeichnet. Anschliessend wird diese Seite auch angezeigt: SCREEN 9,,1-ascreen,1-ascreen. Und ascreen selbst wird aktualisiert: ascreen=1-ascreen.
'Test fuer zwei Bildschirmseiten 'Seite 1 wird angezeigt, auf Seite 0 wird gezeichnet. SCREEN 9, , 0, 1 FOR ix = 0 TO 31 LINE (ix * 20, 0)-(ix * 20, 479) NEXT ix 'Nach dem Tastendruck wird Seite 0 angezeigt: WHILE (INKEY$ = ""): WEND SCREEN 9, , 0, 0
Das Wechseln der Bildschirmseiten integriert man am Besten in cubedraw().
Und? Nun sollte das Bewegen des Klotzes richtig flüssig von statten gehen!
Wir kennen in der Geometrie zwei Drehungen: Punktdrehungen und Achsdrehungen. Wir beschäftigen uns mit Achsdrehungen:

Eine Achse ist einfach eine Linie. Wir benötigen also nur zwei Punkte, durch die diese Linie läuft, nennen wir sie x und y. Zweckmässigerweise werden sie vom Typ point3dtyp sein. Für die Achse definieren wir also einfach einen weiteren Typ "axetyp":
TYPE axetyp x: POINT3dtyp y: POINT3dtyp END TYP
Für den Anfang sollten wir x in den Nullpunkt unseres Klotzes legen, da unsere Drehung so einfacher zu rechnen ist.
Die Achse schliessen wir in die Definition unseres Klotzes mit ein.
TYPE cubetyp p1 AS POINT3dtyp p2 AS POINT3dtyp p3 AS POINT3dtyp p4 AS POINT3dtyp p5 AS POINT3dtyp p6 AS POINT3dtyp p7 AS POINT3dtyp p8 AS POINT3dtyp axe AS axetyp END TYPE
Beispiel einer Initialsierung wäre z.B.
cube.axe.x.x1=cube.p1.x1 cube.axe.x.x2=cube.p1.x2 cube.axe.x.x3=cube.p1.x3 cube.axe.y.x1=cube.p7.x1 cube.axe.y.x2=cube.p7.x2 cube.axe.y.x3=cube.p7.x3
Dann verliefe die Drehachse diagonal durch den Klotz. Aber das können Sie natürlich nach Lust und Laune wählen!
Der Satz des Pythagoras
Nun kommen wir zu einem Stück Mathe, von dem Sie wahrscheinlich nicht dachten, dass Sie dem noch einmal begegnen werden: Zum Satz von Pythagoras. Und zwar in Verbindung mit der Vektordarstellung unserer Achse.
Die Zweipunktedarstellung ist sehr angenehm, wenn man die Achse sich vorstellen und definieren soll. Für die Rechnung der Drehung benötigen wir jedoch die Angabe der Linie in einer anderen Form. Wir haben weiter vorne ja schon gelernt, dass ein "Vektor" die Angabe eines "Raumschritts" und damit einer Richtung ist: "Soundsoviel Schritte in x1, soundsoviel Schritte in x2, soundsoviel Schritte in x3". Ein Vektor mit (1,2,2) würde z.B. bedeuten: "1 Schritt in Richtung x1, 2 Schritte in Richtung x2, 2 Schritte in Richtung x3". Es ist eine Richtungsangabe, von wo aus diese Schritte passieren, ist egal.
Diesen Vektor können wir aus unseren zwei Punkten leicht generieren: Wir ziehen einfach die einzelnen Koordinaten voneinander ab: v.x1=y.x1-x.x1 usw.. Das grössere Problem ist, dass die Länge des Vektors genau eins sein muss. Das nennt man dann einen "Einheitsvektor". Wie machen wir das? Dazu brauchen wir nun Herrn Pythagoras. Er sagt uns, wenn wir x1 in Richtung 1 und x2 in die dazu senkrechte Richtung 2 marschieren, wie lange dann die Diagonale ist:

Die Länge unseres Vektors im Zweidimensinionalen wäre also d. Und da wir im Dreidimensionalen arbeiten, heisst es halt für d:

Wenn nun unser Vektor d lang ist, dann kriegen wir ihn auf die Länge eins, indem wir jede Koordinate um 1/d kürzen. Unser kleiner Minibeweis:

Damit haben wir den "Baustoff" für unseren Einheitsvektor zusammen. Wir können das in einer SUB einheitsvektor(v as point3dtyp) zusammenschreiben. In v speichern wir den Vektor. Die Koordinaten von v werden dann auf Einheitslänge umgerechnet:
DIM d AS DOUBLE d = SQR(v.x1^2+v.x2^2+v.x3^2) IF (d>0) v.x1=v.x1/d v.x2=v.x2/d v.x3=v.x3/d ELSE d=-1 END IF einheitsvektor=d
Fertig. Und schon haben wir unseren Achseneinheitsvektor.
Der nächste Teil ist einfach nur eine längliche Formel. Sie nennt sich "Drehmatrix" oder "Rotationsmatrix". Geben Sie diesen Begriff einmal in die Wikipedia ein und Sie erhalten die fertige Drehmatrix. Da wimmelt es von Cosinussen und Sinussen usw. Wir müssen nicht verstehen, warum sie so aussieht, wir müssen sie nur in BASIC umsetzen und wir müssen wissen, wie man sie benutzt. Da wir inzwischen unseren Achseneinheitsvektor haben, ist das auch nicht weiters schwierig. Um Ihnen die Tipparbeit zu erleichtern, gebe ich Ihnen hier die Umsetzung in QBASIC gleich fertig an:
FUNCTION rotmatr1! (x1 AS DOUBLE, x2 AS DOUBLE, x3 AS DOUBLE, alpha AS DOUBLE, adir AS DOUBLE, a2 AS DOUBLE, a3 AS DOUBLE) DIM r AS DOUBLE r = (COS(alpha) + a1 ^ 2 * (1 - COS(alpha))) * x1 + (a1 * a2 * (1 - COS(alpha)) - a3 * SIN(alpha)) * x2 r = r + (a1 * a3 * (1 - COS(alpha)) + a2 * SIN(alpha)) * x3 rotmatr1 = r END FUNCTION FUNCTION rotmatr2! (x1 AS DOUBLE, x2 AS DOUBLE, x3 AS DOUBLE, alpha AS DOUBLE, a1 AS DOUBLE, a2 AS DOUBLE, a3 AS DOUBLE) DIM r AS DOUBLE r = (a1 * a2 * (1 - COS(alpha)) + a3 * SIN(alpha)) * x1 r = r + (COS(alpha) + a2 ^ 2 * (1 - COS(alpha))) * x2 r = r + (a2 * a3 * (1 - COS(alpha)) - a1 * SIN(alpha)) * x3 rotmatr2 = r END FUNCTION FUNCTION rotmatr3! (x1 AS DOUBLE, x2 AS DOUBLE, x3 AS DOUBLE, alpha AS DOUBLE, a1 AS DOUBLE, a2 AS DOUBLE, a3 AS DOUBLE) DIM r AS DOUBLE r = (a3 * a1 * (1 - COS(alpha)) - a2 * SIN(alpha)) * x1 r = r + (a3 * a2 * (1 - COS(alpha)) + a1 * SIN(alpha)) * x2 r = r + (COS(alpha) + a3 ^ 2 * (1 - COS(alpha))) * x3 rotmatr3 = r END FUNCTION
(Am Besten, Sie übernehmen das via Copy and Paste in Ihr Programm; das vermeidet Tippfehler!)
(a1,a2,a3) ist der Einheitsvektor, (x1,x2,x3) ist der zu drehende Punkt und alpha ist der Drehwinkel.
Es empfiehlt sich, eine weitere Routine "rot3dpoint(p as point3dtyp, adir as point3dtyp, alpha as double)" einzuführen, die die Anwendung der einzelnen Funktionen rotmatr!() auf die Koordinaten von p übernimmt. adir enthält den Achseneinheitsvektor.
Na, Überblick verloren? Was müssen wir nun machen, damit wir den ganzen Klotz drehen können? Ganz einfach: Wir müssen
Nennen wir das rotfig3d(cube as cubetyp, alpha as double) und es ist das Äquivalent zu movefig3d().
Nun können Sie das Steuerungsmenü entsprechend erweitern, um Befehle zur Rotation und z.B. auch um Befehle zur Veränderung der Achslage.
WHILE (a$ <> "q") a$ = "" WHILE (a$ = ""): a$ = INKEY$: WEND IF (a$ = CHR$(0) + "M") THEN dp.x1=3:dp.x2=0:dp.x3=0:CALL movefig3d(cube,dp) IF (a$ = CHR$(0) + "K") THEN dp.x1=-3:dp.x2=0:dp.x3=0:CALL movefig3d(cube,dp) IF (a$ = CHR$(0) + "P") THEN dp.x1=0:dp.x2=3:dp.x3=0:CALL movefig3d(cube,dp) IF (a$ = CHR$(0) + "H") THEN dp.x1=0:dp.x2=-3:dp.x3=0:CALL movefig3d(cube,dp) IF (a$ = "t") THEN dp.x1=0:dp.x2=0:dp.x3=3:CALL movefig3d(cube,dp) IF (a$ = "g") THEN dp.x1=0:dp.x2=0:dp.x3=-3:CALL movefig3d(cube,dp) IF (a$ = "n") THEN CALL rotfig3d(cube,-10) IF (a$ = "m") THEN CALL dotfig3d(cube,+10) WEND
Wenn wir movefig3d() anwenden, dann verschieben wir den Klotz - aber nicht die Drehachse. Das Ergebnis sieht dann lustig aus: Der Klotz dreht sich nicht mehr in sich selbst, sondern in etwa um den Nullpunkt des Koordinatensystems. Was müssen wir tun, damit sich die Drehachse mitbewegt?
An sich ist die Antwort ersteinmal ganz einfach: Einfach die Achskoordinaten mitverschieben. Wir müssten also movefig3d() auch auf die Koordinaten von cube.axe anwenden. Die Sache hat nur einen Haken: Es nutzt nichts. Wenn wir aus den beiden Punkten der Achse wieder einen Einheitsvektor bilden, bleibt dieser Vektor immer derselbe, egal wie wir x und y verschoben haben. Und die Drehmatrix nimmt an, dass dieser Einheitsvektor durch den absoluten Nullpunkt geht.
Die Lösung des Problems heisst dieses Mal in der Fachsprache "Koordinatentransformation". Einfacher gesagt. Wir rechnen temporär die Koordinaten aus, die der Klotz hätte, wenn dessen Achse immer noch im Nullpunkt liegen würde. Dann drehen wir diese Koordinaten. Und rechnen sie anschliessend wieder zurück. Klingt komplizierter als es ist.
Sehr nützlich ist es, für diese Operation eine allgemeine addpoint() und subpoint()-Routine zu haben, die die Koordinaten zweier Punkte addiert und subtrahiert.
Dann hüllen wir unsere rot3dpoint()-Routine durch eine rot3dpoint1()-Routine ein. In dieser wird zuerst die Hintransformation ausgeführt, dann rot3dpoint() aufgerufen und dann die Rücktransformation ausgeführt. Das Ganze sieht dann so aus:
SUB rot3dpoint1(p AS POINT3dtyp, diff AS POINT3dtyp, adir AS POINT3dtyp, alpha AS double) DIM p1 AS POINT3dtyp 'p1=p-diff subpoint p1, p, diff CALL rot3dpoint(p1, adir, alpha) 'p=p1+diff addpoint p, p1, diff END SUB
Und schon haben wir auch dieses Problem gelöst.
Ich hoffe, es fiel Ihnen nicht schwer, aus den einzelnen Bausteinen nun Ihren rotierenden Klotz zusammenzubauen. Wenn Sie es geschafft haben, werden Sie hoffentlich ein bisschen begeistert sein, dass Sie das schaffen konnten. Alles zusammen klang ja höllisch kompliziert. Und wenn Sie im ersten Teil dieses Kurses ("zu Zeiten des C16") vor dieser Aufgabe gestanden wären, hätten Sie nicht eine Sekunde daran gedacht, einen ganzen Kubus in einem 3D-Raum um eine verschobene Drehachse rotieren und dann das Abbild ins Zweidimensionale projizieren zu lassen. Aber dank der Zerlegung in die einzelnen Aufgaben und die Möglichkeit, diese in getrennten Funktionen bearbeiten zu lassen, war es letztendlich nicht schwer, oder? Wahrscheinlich haben Sie sogar Lust auf mehr bekommen. Kann man nun aus mehreren Klötzen eine ganze Figur zusammenbauen? Kein Problem! Kann man einzelne dieser Klötze um eine Achse rotieren und dabei Nachbarklötze "mitnehmen" lassen, so dass "Gelenke" entstehen? Kein Problem! Schwieriger wird es, wenn man die Aussenflächen der Klötze "lackieren" möchte. (Man nennt das in der 3D-Fachsprache "Rendern"). Dann muss man nämlich wissen, welche Flächen aus Sicht des Betrachters vorne und hinten sind. Aber auch das ist ganz und gar kein unlösbares Problem.
Als kleines Ergebnisbeispiel habe ich einen kleinen Kran gebaut. In QBASIC. Genau mit den Routinen, die wir hier besprochen haben. Ohne Zuhilfenahme irgendwelcher weiterer Ressourcen. Um Sie nicht in Versuchung zu führen, liefere ich allerdings nicht den Quellcode, sondern nur ein Kompilat aus - sogar eines für Windows. Wie man das macht, wird Ihnen im folgenden "Freebasic"-Teil verraten.
Für diese Windows-Version sollten Sie allerdings einen einigermassen leistungsfähigen Rechner haben (Pentium4 ab 2 GHz, Athlon XP ab Quantispeed 1500). Der Grund liegt darin, dass Windows zwei Grafiksysteme besitzt, ein einfaches, sehr langsames, vor allem, was Doublebuffer-Grafiken angeht. Und ein schnelles, das s.g. DirectX-System, das hier aber nicht benutzt wird.
Die Bedienung:
Viel Spass!